
Projects
Neural Operators: AI-based solvers for PDEs
PI: Anima Anandkumar (Division of Engineering and Applied Science)
SASE: David Pitt, Scholar
Researchers in the Anima AI + Science Lab develop Neural Operators (NOs), a new class of deep learning models designed to solve partial differential equations (PDEs) more efficiently than traditional numerical methods. NOs have shown significant promise for accelerating simulations in areas such as fluid dynamics, materials science, and climate modeling. The NeuralOperator library provides an open-source, unified framework for training and applying these models, making them accessible to researchers across scientific domains.
Over the course of this project, the NeuralOperator library has been significantly expanded and stabilized. The codebase now has high test coverage, making it more reliable and easier to extend. New geometric models and physics-informed learning schemes have been added, enabling the application of NOs to a wider range of physical problems. The library now supports benchmark datasets commonly used in the PDE community through standardized, unified interfaces, as well as additional data formats and a public dataset repository on Zenodo. These improvements, along with new modular frameworks for automated training and advanced meta-algorithms for complex training schemes, have made it easier for researchers to prototype, test, and deploy NO models. As a result, NeuralOperator has been used in more than ten peer-reviewed papers in the last two years, and the repository has earned more than 2,700 stars and 600 forks on GitHub.
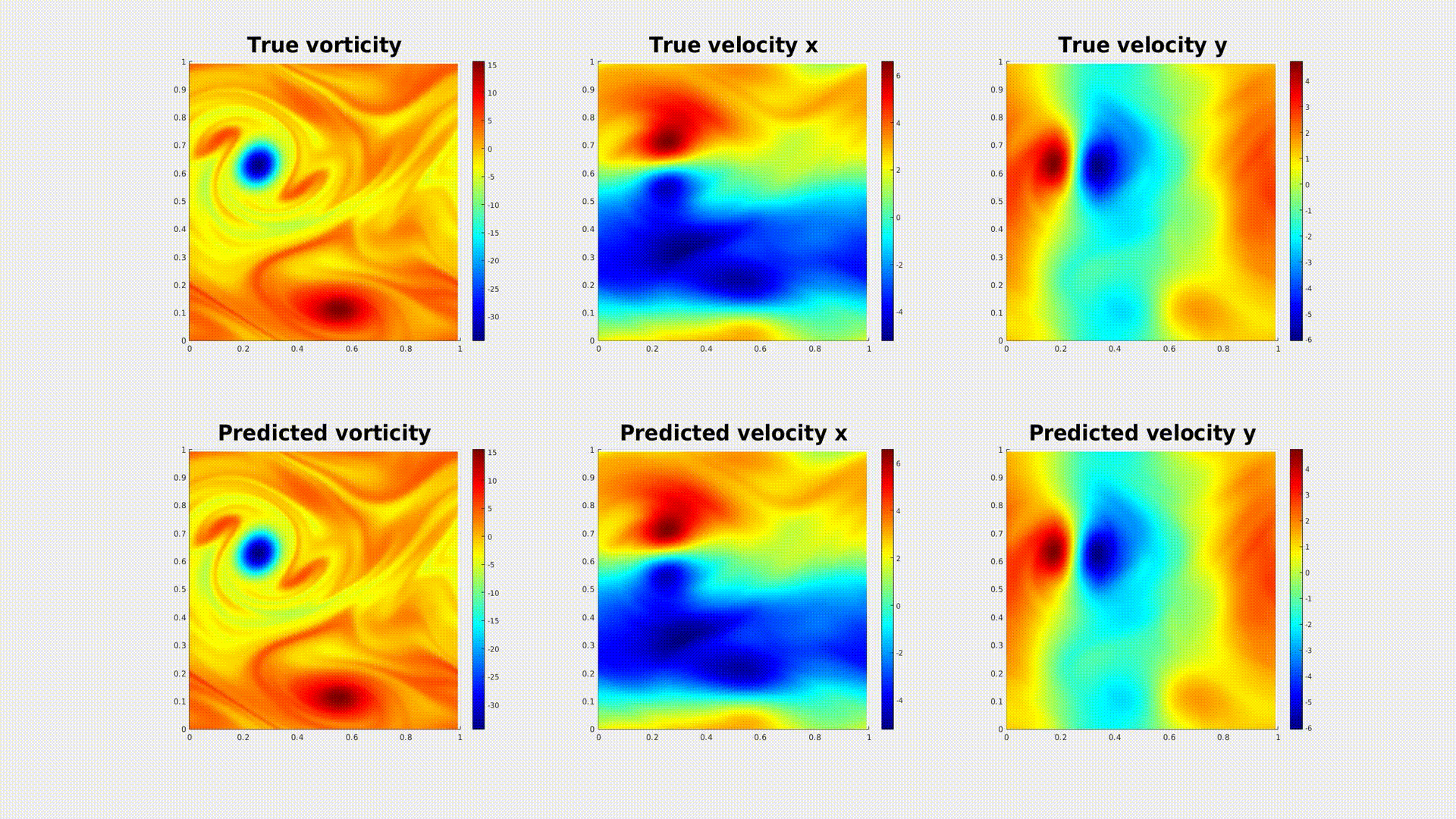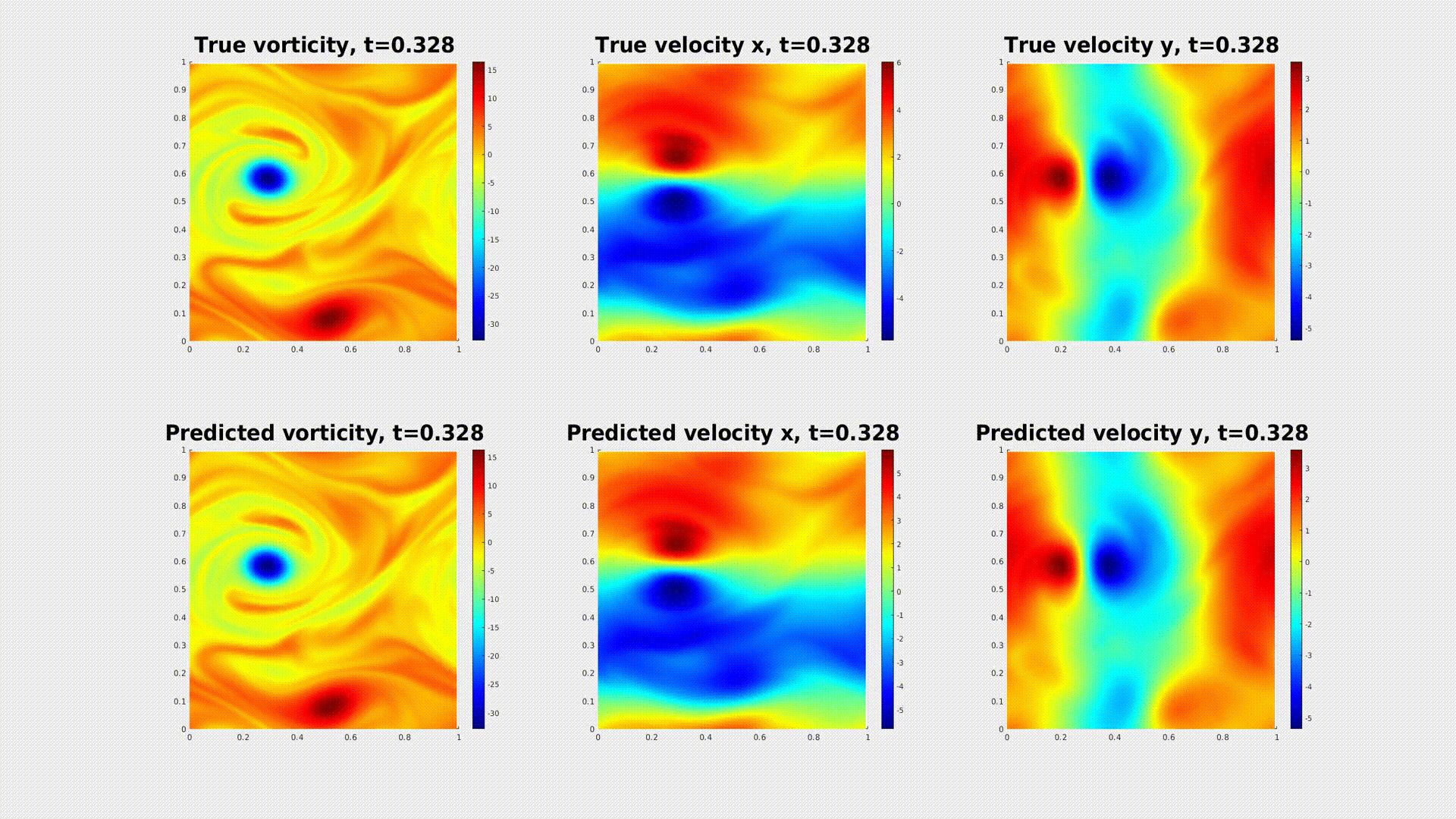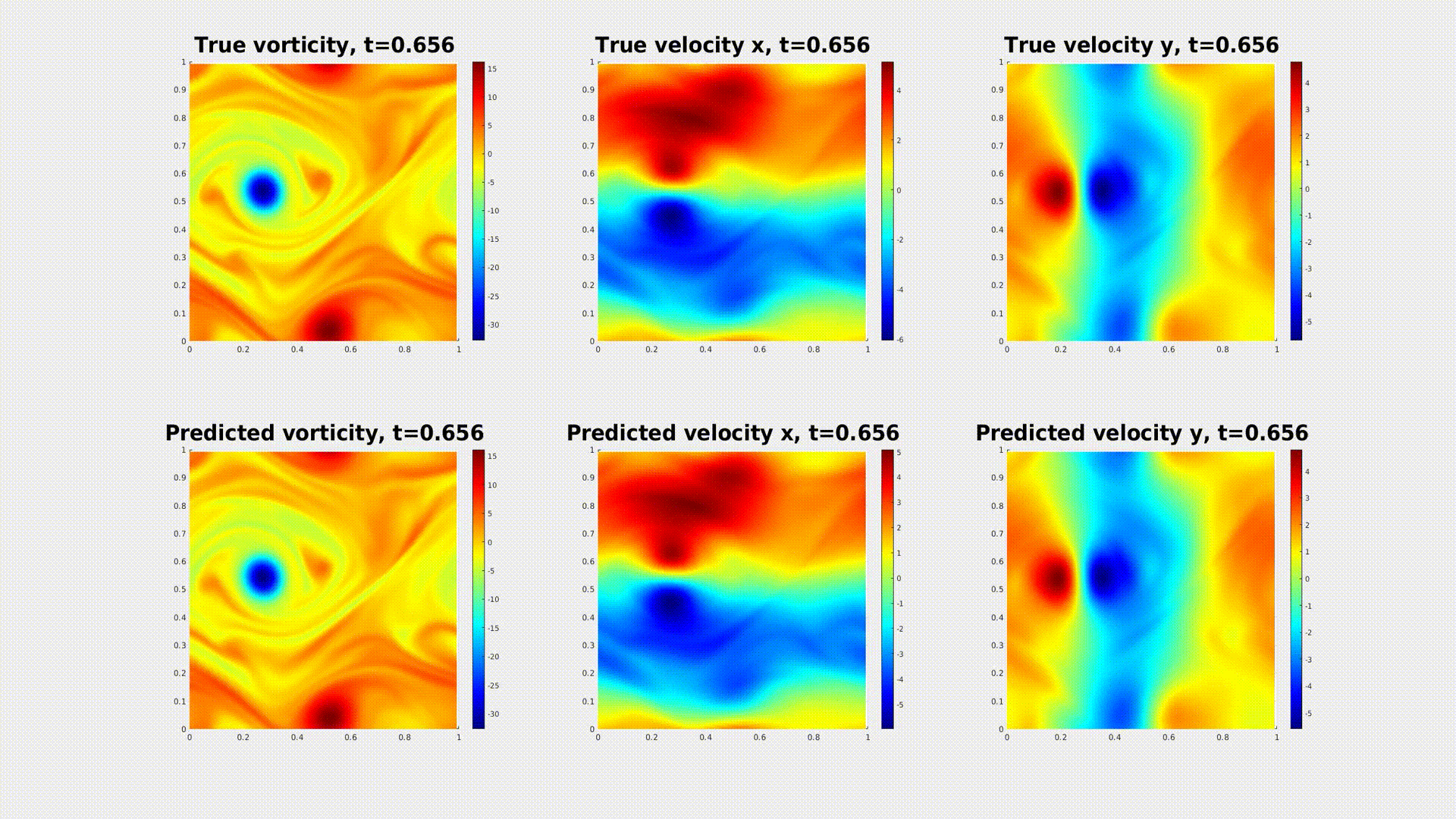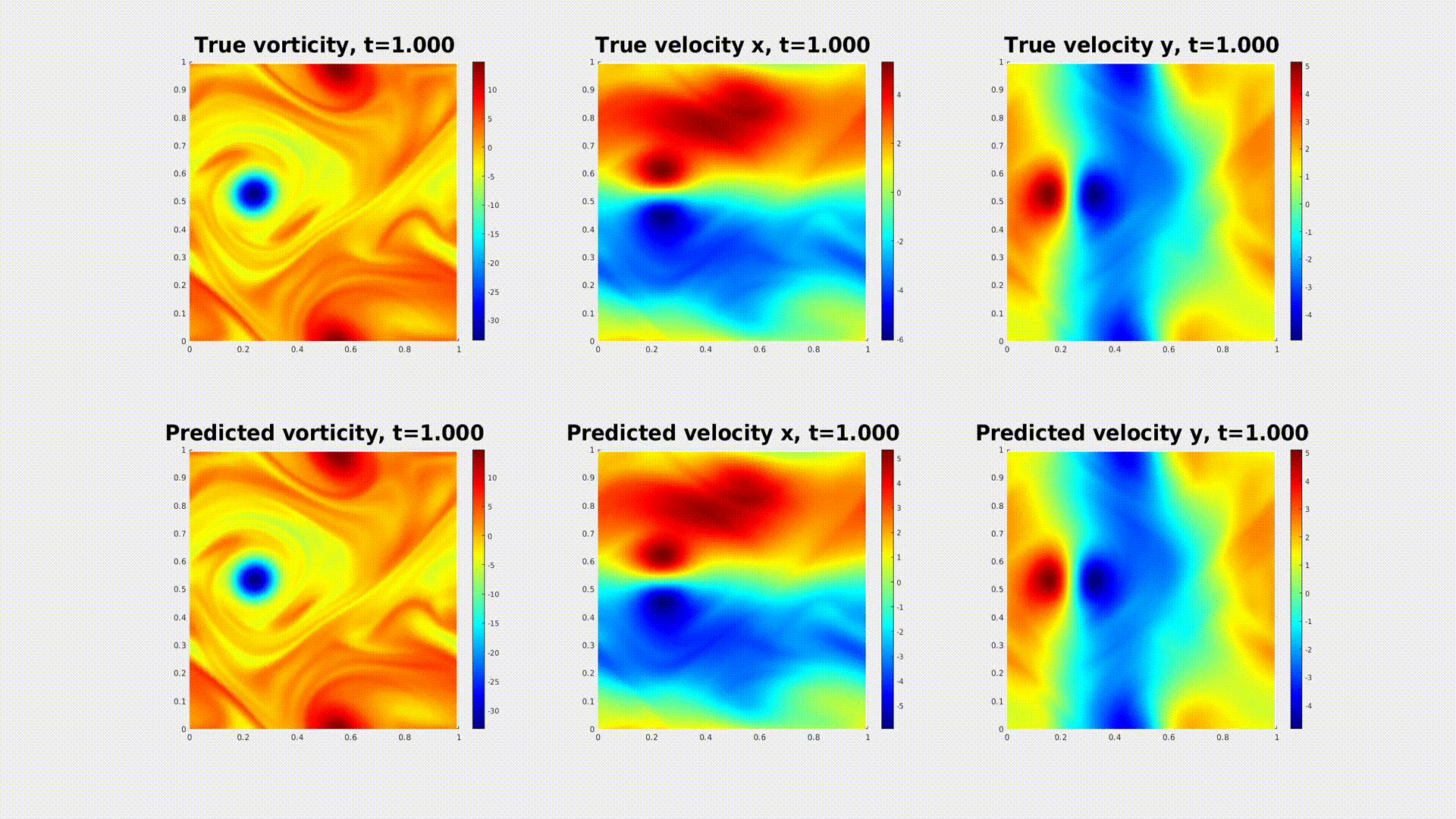
Caption: A physics-informed neural operator generates a prediction of turbulent micro-scale fluid flow in 2D. [More Information]
The library's documentation has also been fully refreshed. It now includes a gallery of interactive examples that allow users to quickly explore core functionality and adapt NO workflows to their specific problems. Together, these improvements have made NeuralOperator a reliable and widely adopted tool for accelerating scientific computing with machine learning.
NeuralOperator repository on GitHub
NeuralOperator docs website